As we have seen in this series, the real secret of the super rich is neither positive thinking nor dark forces at work. It is nonlinearity. The basic bell curve distribution comes from adding assorted random variables together, and as we have seen, there is no way to map such a bell curve distribution to the actual wealth distribution of the United States (or probably any other nation). The underlying logic of the bell curve doesn’t even make sense if you think about it. If Bill Gates was a poor programmer or a poor businessman, he would be simply half as rich. He would not be rich at all. (Or at least not rich as a software entrepreneur.) These factors multiplied each other.
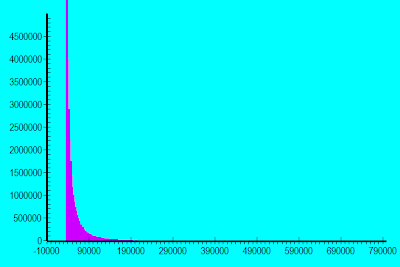
I modeled the effect of multiplying abilities/drives/luck factors together in Part 3. To review, here is the graph I get when I take five random factors, multiply them together and normalize to match median household income and a standard deviation which divides the bottom two quintiles properly.
We get a nice bulge near the median and a tail off to the right, but we still don’t get any super rich people. My model estimated only 56 people barely breaking a half million people per year. (This estimate is quite noisy; only one dice roll out of a million landed in this bin.)
Let’s think back to our Bill Gates model. If he was half as good a programmer, he wouldn’t simply have had half as good a business; he wouldn’t have gotten into writing interpreters and operating systems at all. If his parents had been half as well off, he wouldn’t have had half the practice writing software as a child. He would have had none at all. If he had too little interest/ability in business, he would have stayed in Harvard and probably became an academic or high paid programmer working for someone else. For many of the factors which went into making Bill Gates rich, there is a threshold value below which his life would have followed a very different trajectory.
And above the thresholds, the difference between good and great were still enormous. Had he and his friends done a less good job writing BASIC interpreters, Microsoft would have been just another flash in the pan software house. Gates and company abstracted out the hardware dependent portions of their interpreter so they could have a new interpreter ready for each new machine faster than any competitor or in-house programmers could. Microsoft got big because they were very competent – combined with a willingness to compromise quality in order to make computing affordable.
Since dealing with multiple operating systems is quite a bother for both customers and software designers, operating system design is a winner-take-all business. The difference between best and second best is huge, and the difference between best the fourth best is truly enormous. Similar economies apply to radio and pre-cable television. Ditto for sports. When the number of niches is few, those who win win big.
To model these dynamics simply, I took the code from my previous experiment and squared the rolls for the individual factors. That is, for each factor I rolled 5 twenty-sided dice, added the results together and squared the total. Then these factors were multiplied together as before and the results renormalized to match the target median and standard deviation. The result was:
Now we are getting somewhere: heavy clustering around the middle with a tail off to the right. When I look at the underlying chart, my top nonzero bin is now at 1.5 million dollars per year, and I have four bins breaking a million dollar income with an estimated 500 people per bin. This is still too low, however, so I then tried cubing the factors to get:
This gets me a top bin of around four million dollars per year, but only 50 people in that bin. The model is better, but still doesn’t fully account for the super rich. I could get more aggressive yet (worth doing for winner-take-all economics) or play with more input factors (talents, drive, luck,etc.) but I have another nonlinearity to cover in the next post.
Also, the two curves above don’t go down far enough. We get some rich at the cost of losing the working poor. A higher-fidelity model would take into account the fact that there are two economies: one with high barriers to entry and winner-take-all economics and another where gain is linear or less with effort; i.e., the ordinary wage and Main St. economy.
Applying the Secret
This post is running long, so I’ll leave it primarily as a meditation for the reader to figure out how to apply the knowledge above. Here are a few hints.
If you want to get really rich, look for barriers to entry and cross them. In other words, don’t look for the free money making opportunities. Those lead to mediocre incomes unless you happen to be lucky enough to get in early. Low barrier to entry income can be good for seed money and gaining experience, but the real bucks must come from beating out some real competition.
If you don’t like the enormous wealth gap we have today, you have two ideas you can apply. First, look to lower barriers to entry. This requires going against the modern liberal impulse to craft complex legislation that only an expensive lawyer can understand. If going into a business requires expensive legal and/or engineering consultants, only people who can afford these expensive professionals will be able to compete. Second, look to divide up the economy into more independent niches. For example, federalizing intrastate commerce law gives economies of scale to multi-state corporations such as Wal Mart. Having different laws in each state gives smaller operations a fighting chance.
But neither of these paths will bring the wealth gap down to liberal targets unless we deal with the final nonlinearity: the rich get paid just for being rich. I’ll explain more in the next post.
Posts
